The conditional or non conditional stability (limited time step) of the Newmark's algorithm depends on the value of the parameters $\beta$ and $\gamma$. To stay in the non conditional stability zone, two parameters $\alpha$ and $k$ which scan this zone must be introduced: \[\beta=\frac{(1+\alpha)^2}{4}\] \[\gamma=\frac{1}{2}+\alpha k\] With $\alpha>0$ and $0 \leq k \leq 1$ in the non conditionally stable zone.

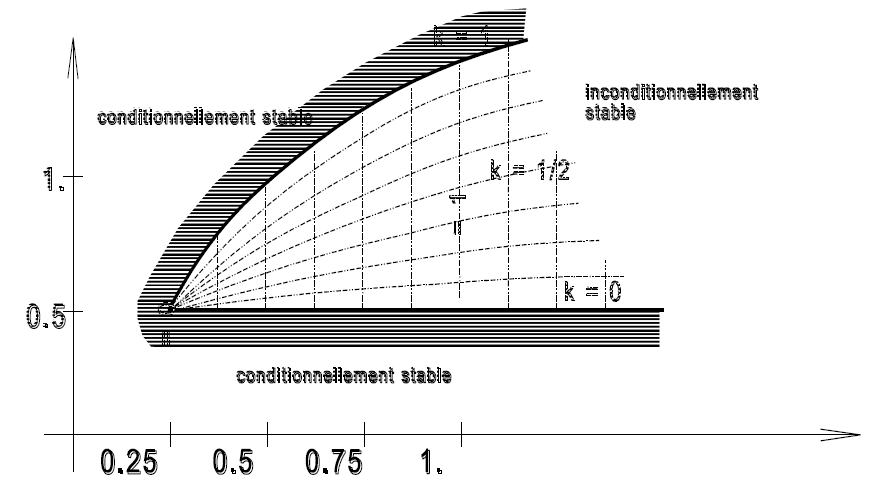
Moreover, a numerical damping appears if $\gamma \neq 0.5$ and it is all the more important as $\gamma$ is different from 0.5 and as the time step is great relating to the fundamental period.
If $\beta$ is greater than 0.25 and $\gamma$ greater than 0.5, a frequency distortion appears, all the more great as the time step is great.
That's why, one advises to take: $0 \leq \alpha \leq 1$ and $0 \leq k \leq 0.5$
This is valid in the linear case. In the non linear case, some modifications may appear.