User Tools
Sidebar
Table of Contents
Appendix 10: Dynamics parameters
Choice of Newmark parameters
The conditional or non conditional stability (limited time step) of the Newmark's algorithm depends on the value of the parameters $\beta$ and $\gamma$. To stay in the non conditional stability zone, two parameters $\alpha$ and $k$ which scan this zone must be introduced: \[\beta=\frac{(1+\alpha)^2}{4}\] \[\gamma=\frac{1}{2}+\alpha k\] With $\alpha>0$ and $0 \leq k \leq 1$ in the non conditionally stable zone.
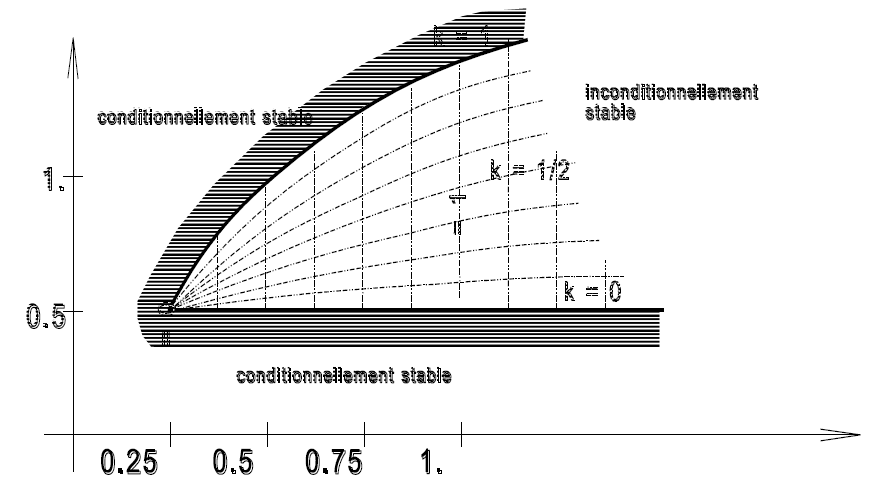
Moreover, a numerical damping appears if $\gamma \neq 0.5$ and it is all the more important as $\gamma$ is different from 0.5 and as the time step is great relating to the fundamental period.
If $\beta$ is greater than 0.25 and $\gamma$ greater than 0.5, a frequency distortion appears, all the more great as the time step is great.
That's why, one advises to take: $0 \leq \alpha \leq 1$ and $0 \leq k \leq 0.5$
This is valid in the linear case. In the non linear case, some modifications may appear.


Choice of INITV
Before any iteration, there are various ways to estimate the geometry at the end of the step $X_B$.
Considering: $X_B=X_A+\Delta X$
with $X_A$ = geometry at the beginning of the step
$X_B$ = geometry at the end of the step
$\Delta X$ = increment of displacements
The following choices are available:
| INITV | Increment of displacements | Method |
|---|---|---|
| \[= 0\] | \[\Delta X = 0\] | Most effective choice |
| \[= 1\] | \[\Delta X = \dot{V}_0 \Delta t + \ddot{V}_0 \frac{\Delta t^2}{2}\] | Central difference method |
| \[= 2\] | \[\Delta X = \dot{V}_0 \Delta t + \frac{1}{2} \ddot{V}_0 \Delta t^2 \left(1-\frac{2 \beta}{\gamma}\right)\] | Newmark's algorithm with $ \dot{V}_1=\dot{V}_0$ |
| \[= 3\] | \[\Delta X = \dot{V}_0 \Delta t \left(1-\frac{\beta}{\gamma}\right) + \frac{1}{2} \ddot{V}_0 \Delta t^2 \left(1-\frac{2 \beta}{\gamma}\right)\] | Newmark's algorithm with $ \dot{V}_1=0$ |
| \[= 3\] | \[\Delta X = \dot{V}_0 \Delta t + \frac{1}{2} \ddot{V}_0 \Delta t^2 \left(1-2 \beta\right)\] | Newmark's algorithm with $ \ddot{V}_1=0$ |
With:
- $\dot{V}_0$ = speeds at the beginning of the step
- $\ddot{V}_0$ = accelerations at the beginning of the step
- $\dot{V}_1$ = speeds at the end of the step
- $\ddot{V}_1$ = accelerations at the end of the step
