User Tools
Sidebar
This is an old revision of the document!
Table of Contents
Appendix 8: Water retention curves, water and air relative permeability curves and thermal conductivity function
Water retention curves
- ISR = 0 \[S_w=1\]
- ISR = 1 \[S_w = S_{r,field}-CSR1\left(\frac{s}{CSR3}\right)^{CSR2}\] With: $s=p_a-p_w$
Example: \[CSR1 = 0.09686 \\ CSR2 = 2.428 \\ CSR3 = \rho_w.g.C^{ste}\] - ISR = 2 \[ -\frac{s}{\rho_wg} = \begin{cases} -10.214\exp(-15.27S_w+6.062) & \quad \text{if } 0.1<S_w<1 \\ -10.214\exp(314.84S_w^2-78.24S_w+9.21) & \quad \text{if } 0<S_w<0.1 \end{cases}\]
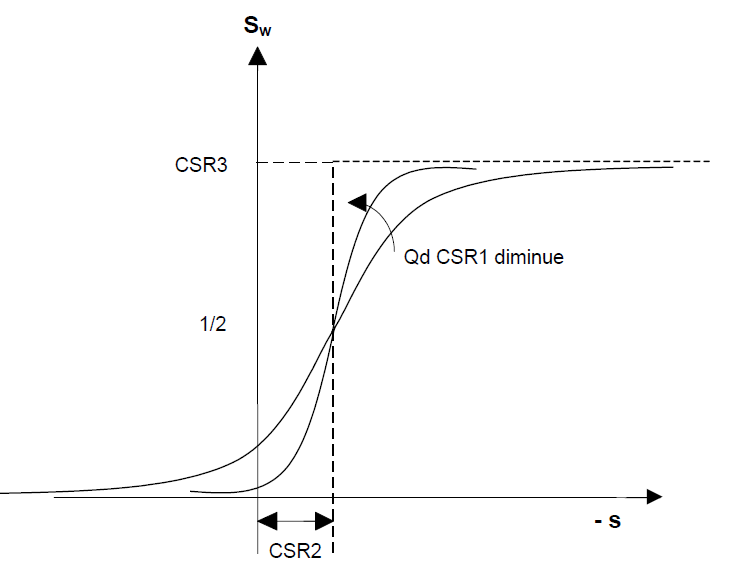
- ISR = 3 \[ S_e(p_c)= \begin{cases} CSR3+\left(1+\left(\frac{p_c}{CSR1}\right)^{\frac{1}{1-CSR2}}\right)^{-CSR2} & \quad \text{if } p_c>0 \\ 1 & \quad \text{if } p_c \leq 0 \end{cases}\] Example: \[CSR1 = 10^7 Pa \\ CSR2 = 0.412 \\ CSR3=0\]
- ISR = 4 \[S_w = \begin{cases} CSR1 ln\left(\frac{s}{10^6}\right) +CSR2 & \quad \text{if } 0.26 \text{ MPa}<s<222\text{ MPa} \\ S_{res} & \quad \text{if } s>222 \text{ MPa} \\ S_{r,field} & \quad \text{if } s<0.26 \text{ MPa}\end{cases}\]
- ISR = 5 \[S_w = S_{res} + (S_{max}-S_{res})\left(1+\left(\frac{s}{CSR1}\right)^{CSR2}\right)^{-\left(1-\frac{1}{CSR2}\right)}\]
- ISR = 6 \[S_w = S_{res}+\frac{CSR3(S_{r,field}-S_{res})}{CSR3+(CSR1*s)^{CSW2}}\]
- ISR = 7 \[S_w=\frac{CSR1 \log(s*10^{-6})+CSR2}{100} \\ \text{If } S_w<S_{res} \Rightarrow S_w = S_{res} \\ \text{If } S_w>S_{r,field} \Rightarrow S_w = S_{r,field}\]
- ISR = 9: Quasi-saturated soils
- ISR = 17 (EPFL-LMS, Lausanne)
Parameter correspondance:
CSW1=$\beta_h$
CSW2=$s_{hys}$
CSW3=$\theta_T$
CSW4=$\theta_e$
CSW5=RETINI
An elasto-plastic approach is used to describe the curve of retention of the soil. This implies two plastic mechanisms:
→ A mechanism activated during drying $f_{dry}=s-s_d=0$
→ A mechanism activated during the wetting $f_{wet}=s_d s_{hys} - s=0$
Where $s_d$ is the drying limit and $s_{hys}$ is a parameter defining the opening of the hydric hysteresis. When a mechanism is activated, $s_d$ evolves according to the following exponential law: $s_d=s_{d0}\exp(-\beta_h \Delta S_w)$
The effects of mechanical deformation and of temperature on the retention curve are considered through the evolution of the entering air suction: \[s_e=s_{e0}\exp(-\beta \Delta S_w)\left[1-\theta_T\log(T/T_0)-\theta_e \log(1-\varepsilon_v)\right]\] In order to characterize the initial degree of saturation inside the hydric hysteresis, the RETINI parameter is used. At the initial state, for a given suction, if RETINI = 0, the point is on the drying curve; if RETINI = 1, the point is on the wetting curve. RETINI can also take a value between 0 and 1. In that case, the saturation degree is determined using a linear interpolation between the drying curve and the wetting curve. - ISR = 18 (EPFL-LMS, Lausanne)
Parameter correspondance:
CSW1=$s_{D0}$
CSW2=$\kappa_H$
CSW3=$\beta_H$
CSW4=$\pi_H$
CSW5=RETINI
The water retention curve is modeled using an elasto-plastic approach with kinematic hardening (ACMEG-s model, LMS, EPFL) The yield surface delimiting the elastic domain takes the following form: \[f=\left\Vert ln\left(\frac{s}{s_D}\right)+\frac{1}{2}ln\left(\frac{s_{D0}}{s_{eH}}\right)\right\Vert - \frac{1}{2} ln \left(\frac{s_{D0}}{s_{eH}}\right)\] The saturation degree $S_w$ can be decomposed in an elastic part $S_w^e$ and a plastic part $S_w^p$: \[S_w = S_w^e+S_w^p\] The elastic part is defined by parameter $\kappa_H$ \[S_w^e=1- \frac{1}{\kappa_H}ln\frac{s}{s_{eH}}\] The plastic part is defined by: \[S_w^p=S_w^D-\frac{1}{\beta_H}\ln\frac{s}{s_D}\] The saturation degree cannot be higher than 1 or lower than $S_{res}$.
The yield surface delimiting the elastic domain takes the following form: \[f=\left\Vert ln\left(\frac{s}{s_D}\right)+\frac{1}{2}ln\left(\frac{s_{D0}}{s_{eH}}\right)\right\Vert - \frac{1}{2} ln \left(\frac{s_{D0}}{s_{eH}}\right)\] The saturation degree $S_w$ can be decomposed in an elastic part $S_w^e$ and a plastic part $S_w^p$: \[S_w = S_w^e+S_w^p\] The elastic part is defined by parameter $\kappa_H$ \[S_w^e=1- \frac{1}{\kappa_H}ln\frac{s}{s_{eH}}\] The plastic part is defined by: \[S_w^p=S_w^D-\frac{1}{\beta_H}\ln\frac{s}{s_D}\] The saturation degree cannot be higher than 1 or lower than $S_{res}$.
The entering air suction $s_{eH}$ evolves with the total volumic deformation: \[s_{eH}=s_e+\pi_H*\varepsilon_v\] In order to characterize the initial degree of saturation inside the hydric hysteresis, the RETINI parameter is used. At the initial state, for a given suction, if RETINI = 0, the point is on the drying curve; if RETINI = 1, the point is on the wetting curve. RETINI can also take a value between 0 and 1. In that case, the saturation degree is determined using a linear interpolation between the drying curve and the wetting curve. - ISR = 19 - idem as ISR = 5 with the addition of AIREV in the van Genuchten formulation: \[S_w = \begin{cases} 1 & \quad \text{if } s < \text{AIREV} \\ S_{res}+(S_{max}-S_{res})\left(1+\left(\frac{s-AIREV}{CSR1}\right)^{CSR2}\right)^{-\left(1-\frac{1}{CSR2}\right)} & \quad \text{if } s > \text{AIREV} \end{cases}\]
- ISR = 26 Double structure mechanism adsorption: \[e_w=e_{wM}+e_{wm}\] \[e_w=e_m \exp \left(-(C_{ads}s)^{n_{ads}}\right) + (e-e_m) \left[1+\left( (e-e_m)\frac{s}{A}\right)^n\right]^{-m} \] \[S_r=\frac{e_w}{n}\] $n$=porosity
CSR1 = $A$
CSR2 = $m$
CSR3 = $n$
CSR4 = $C_{ads}$
CSR5 = $n_{ads}$
- ISR = 53 Van Genuchten model (ISR=5) with hysteresis implemented.
The main water retention curves (d=drying, w=wetting) are, according to the Van Genuchten model: \[S_{ed} = S_{res} + (S_{max}-S_{res}) \left[+ 1 \left(\frac{s}{a_d}\right)^{n_d}\right]^{-m_d}\] \[S_{ew} = S_{res} + (S_{max}-S_{res}) \left[+ 1 \left(\frac{s}{a_w}\right)^{n_w}\right]^{-m_w}\]
The hysteresis is then defined by: \[\frac{\partial S_{es}}{\partial s} (\text{wetting}) = \left(\frac{s_w}{s}\right)^b\left(\frac{\partial S_{ew}}{\partial s}\right) \text{ with } s_w = a_w \left(S_e^{-1/m_w}\right)^{1/n_w}\] \[\frac{\partial S_{es}}{\partial s} (\text{drying}) = \left(\frac{s_d}{s}\right)^{-b}\left(\frac{\partial S_{ed}}{\partial s}\right) \text{ with } s_d = a_d \left(S_e^{-1/m_d}\right)^{1/n_d}\]
And therefore: \[S_e^{t+1} = S_e^t + \left(\frac{\partial S_{es}}{\partial s}\right)\times ds\]
Water relative permeability
- IKW = 0 \[k_{rw} = 1\]
- IKW = 1 \[k_{rw} = CKW3 - CKW1 (1-S_{r,w})^{CKW2}\] Example: CKW1 = 2.207; CKW2 = 0.953; CKW3 = 1
- IKW = 2 \[k_e^{rel} (S_e) = \left(1+\left(S_{r,w}^{CKW1} - 1\right)^{CKW2}\right)^{-1}\] Example: Momas: CKW1 = -2.429; CKW2 = 1.176
- IKW = 3 \[k_{r,w} = \begin{cases} \exp(CKW1*S_w+CKW2*S_w^2) & \quad \text{if } S_w \geq S_{res} \\ k_{r,min} & \quad \text{if } S_w<S_{res} \end{cases} \]
- IKW = 4 \[k_{r,w} = \begin{cases} \frac{(S_w-S_{res})^{CKW1}}{(S_{r,field}-S_{res})^{CKW2}} & \quad \text{if } S_w \geq S_{res} \\ k_{r,min} & \quad \text{if } S_w<S_{res} \end{cases} \] Example: $CKW1 = 4$; $CKW2 = 4$; $S_{r,field} = 1$; $S_{res}=0.1$
- IKW = 7 \[k_{rw}=\sqrt{S_{rw}} \left(1-\left(1-S_{rw}^{\frac{1}{CKW1}}\right)^{CKW1}\right)^2\]
- IKW = 8 \[k_{rw} = S_{rw}^3\]
- IKW = 9 \[k_{rw}=\sqrt{S_{we}} \left(1-\left(1-S_{we}^{\frac{1}{CKW1}}\right)^{CKW1}\right)^2\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\] \[S_{rw,res}=CKW2\] \[S_{rg,res}=CKW3\]
Air relative permeability
- IKA = 0 \[k_{ra}=1\]
- IKA = 1 \[k_{ra} = (1-S_e)^{CKA1}(1-S_e^{CKA2})\] \[S_e=\frac{S_{rw}-S_{rw,u}}{1-S_{rw,u}}\] Example: CKA1 = 2; CKA2 = 5/3
- IKA = 2 \[k_{r,a}=CKA1\]
- IKA = 3 \[S_e = \frac{S_{r,w}-S_{r,u}}{1-S_{rw,u}} \\ \begin{cases} \text{If } S_e<0 \Rightarrow S_e = 0 \\ \text{If } 0<S_e<0.55 \Rightarrow k_{ra}=(0.55-S_e)^{CKA1}(1-S_e^{CKA2}) \\ \text{If } S_e>0.55 \Rightarrow k_{ra}=k_{rmin} \end{cases} \] Remark: \[k_{w,effectif}=k_{f,intrinsic}k_{rw} \\ k_{a,effectif}=k_{f,intrinsic}k_{aw}\]
- IKA = 6 \[k_{ra}=\sqrt{1-S_{r,w}}\left(1-S_{r,w}^{\frac{1}{CKA1}}\right)^{2CKA1}\]
- IKA = 7 \[k_{ra}=\sqrt{1-S_{we}}\left(1-S_{we}^{\frac{1}{CKA1}}\right)^{2CKA1}\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\] \[S_{rw,res}=CKA2\] \[S_{rg,res}=CKA3\]
- IKA = 8 \[k_{ra}=CKA2(1-S_{we})^{CKA1}\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\]
Thermal conductivity
| ITHERM | $\Gamma_T$ |
|---|---|
| \[1\] | \[nS_w\Gamma_w+nS_a\Gamma_a+(1-n)\Gamma_s\] |
| \[2\] | \[CLT1*S_w +CLT2\] |
| \[3\] | \[CLT1 -\frac{CLT2}{1 + exp\left(\frac{S_w -CLT3}{CLT4}\right)}\] |