The Lagamine Inverse code allows the computation of parameter sensitivity through a semi-analytical calculation. This implementation does not fundamentally change the code, but the simulation with Lagamine Inverse will be made so as to obtain both a reference finite element curve and the derivative of this curve with respect to the specified parameters.
To compute the derivative of the curve with respect to parameters, Lagamine will run one reference simulation with the input parameters and 2 additional simulations for each optimized parameter: one with a positive and on with a negative perturbation applied to the parameter (see OPTIM Description).
The values of the reference curve and its derivatives are put in a *.sm file at each iteration. When the Lagamine Inverse is used, the parameters specified by the user in the *.ia file are not read from the *.lag file but from the *.op file.

In order to launch a simulation using the Lagamine Inverse, several things are necessary:

1. Modification of the IOPT parameter in the loading file *ex.dat;
2. Implementation in the Lagamine subroutines INVA.F and WSENSM.F to specify the finite element curves to use;
3. Creation of *.ia file and *.op file indicating the number of finite element curve, the parameters to be optimized, their initial values, …

In the *ex.dat file, the parameter IOPT (ninth parameter on the first line) must be set to 1 to activate the Lagamine Inverse simulation. It is also necessary to indicate an IDENT (5th parameter of first line) that allows the user to specify his curve in INVA.F and WSENSM.F (see figure 1).

Fig. 1: Example of *ex.dat file with activation of Lagamine Inverse

The user must implement in the INVA.F subroutine the finite element curves that will be compared with the experimental curves (for instance, a stress-strain curve). For each time step, subroutine INVA.F is called once for the reference simulation (ISENS=0), and twice for each optimized parameter (ISENS=1 for positive perturbation, ISENS=2 for negative perturbation). This allows to compute for every case the wanted curves $REACTION$ (reference), $REACTION_P$ (positive perturbation), $REACTION_M$ (negative perturbation). The computation of the sensitivity is then done according to the following:
\[DUef_{DX}(I,ILI)=\frac{REACTION_P(I)-REACTION_M(I)}{2*PREC_{IA} *XIAPAR(III,LLL)}\]
Where:

• $DUef_{DX}(I,ILI)$ is the derivatives of the Ith curve with respect to parameter n° $ILI$ (with $ILI=1,NBPAR_{OP}$)
• $REACTION_P(I)$ is the value of the Ith curve with a positive perturbation $PREC_{IA}*XIAPAR(III,LLL)$ on parameter n°$ILI$
• $REACTION_M(I)$ is the value of the Ith curve with a negative perturbation $PREC_{IA}*XIAPAR(III,LLL)$ on parameter n°$ILI$
• $PREC_{IA}$ is the relative perturbation
• $XIAPAR(III,LLL)$ is the value of parameter n°$LLL$ of law n°$III$ to be optimized

4 zones must be modified in the INVA.F subroutine to implement the computation of each reaction and of the derivative. These 4 zones are indicated by comments in the subroutine. Users must implement their curve using their IDENT number.
The first zone is used for the definition of the reference curves ($REACTION(I)$). It is necessary to write an “IF” condition imposing the chosen IDENT and ISENS=0. Users can then define as many curves as they want. The curves are taken from either nodal values (CONEC matrix), from integration point values (SIGVA vector), or from nodal reactions (vector REACT(-ID(Node, DOF))).

Fig. 2: First zone to modify in the INVA.F subroutine
In the case shown in figure 2 with IDENT=4444, the first curve $REACTION(1)$ corresponds to the compression force on a cylinder. The reaction on DOF 2 (Y-direction) at node 205 is the reaction at the pilot node of the foundation in the axisymetric case; this reaction multiplied by $2\pi$ gives the compression reaction on the cylinder. The second curve, $REACTION(2)$, is the coordinate of DOF 1 (X-direction) of node 3 at the end of the time step.

The second and third zones are used for the implementation of the perturbed curves. The second zone is for the positive perturbation ($REACTION_P$) while the third is for negative perturbation ($REACTION_M$). In these cases, matrices CONEC and SIGVA must be replaced respectively by CONEC_PERT_P or CONEC_PERT_M, and SIGVA_PERT_P or SIGVA_PERT_M.

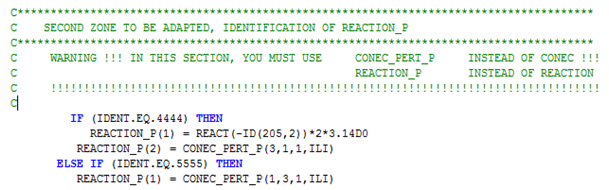Fig. 3: Second zone to modify in the INVA.F subroutine
The fourth zone is for the computation of $DUef_{DX}(I,ILI)$. This calculation is already defined in the code, users simply need to add their IDENT number in the “IF” list as shown in figure 4.

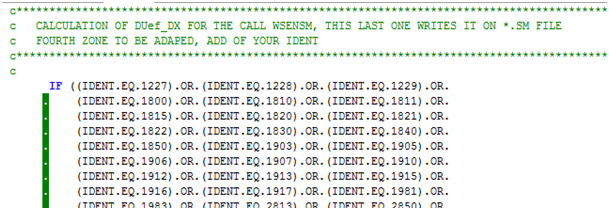Fig. 4: Fourth zone of the INVA.F subroutine