User Tools
Sidebar
Table of Contents
PLXLS
Description
Plane state or axisymmetrical element
For the axisymmetrical element, the axis of symmetry must be the Y axis.
The element is defined by 3, 4, 6, or 8 nodes (see Input file).
For the generalised plane state, 8 nodes of the plane must be defined; the ninth is automatically the last one of the NODES section.
The 4 nodes elements are not of very good quality:
- With 1 integration point, hourglass modes may appear
- With 4 integration points, locking (shear or volumetric) can occur.
 Element type: 9
Element type: 9
Implemented by: J.P. Radu & J.D. Barnichon (1996)
Files
Prepro: PLXLSA.F
Lagamine: PLXLSB.F
Input file
1 - Title
| (A5) | |
|---|---|
| TITLE | “PLXLS” in columns 1 to 5 |
2 - Control
| (3I5) | |
|---|---|
| NELEM | Number of elements |
| ISPMAS | 0 = nothing |
| 1 = if density taken into account (if and only if NTANA=-1) | |
| INSIG | 0 if no initial stresses |
| 1 or 2 if initial stresses | |
| 3 or 4 if residual stresses in cylinder | |
3 - Density (dynamic analysis)
Only if ISPMAS = 1
| (1G10.0) | |
|---|---|
| SPEMAS | Density |
4 - Initial stresses
Only if INSIG > 0
Case 1: INSIG = 1 or 2
If INSIG=1: $\sigma_y=\sigma_{y0}+yd\sigma_{y}$
If INSIG=2: $\sigma_y=min(\sigma_{y0}+yd\sigma_y,0)$
| (4G10.0) | |
|---|---|
| SIGY0 | $\sigma_{y0}$ effective stress $\sigma_y$ at the axes origin |
| DSIGY | Effective stress gradient along Y axis |
| AK0X | $k_0$ ratio $\sigma_x/\sigma_y$ |
| AK0Z | $k_0$ ratio $\sigma_z/\sigma_y$ (if AK0Z=0, AK0Z=AK0X) |
Case 2: INSIG = 3 or 4
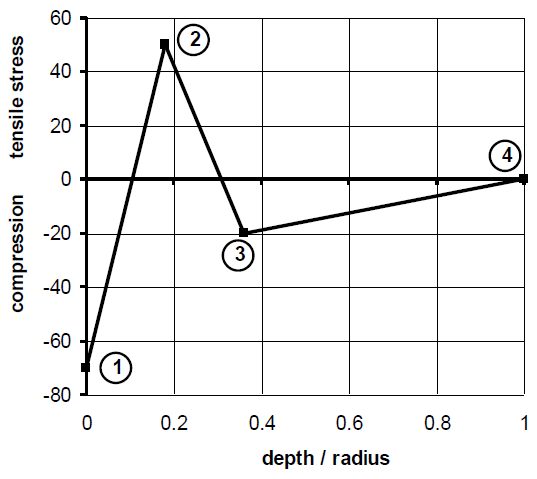
Generally, the radial stress $\sigma_r$ is assumed to be equal to zero.
The longitudinal and circumferencial stresses, $\sigma_L$ & $\sigma_T$, are the same and given, for instance, by the following graph as a function of the depth/radius ratio:
| (6G10.0) | |
|---|---|
| XC | X coordinate of the axis |
| YC | Y coordinate of the axis |
| R1 | radius of the cylinder |
| R2 | radius corresponding to the maximum of tensile stress (point 2) |
| SIGC | maximum compression (observed on the external face of the cylinder) |
| SIGT | maximum tensile stress (point 2) |
The following values are computed automatically:
| R3 | radius corresponding to the point 3 = R2 – ( R1 – R2 ) |
| SIGR3 | stress corresponding to the point 3 = ½ ( SIGT + SIGC ) |
The stress on the axis is equal to zero.
At each integration point, the initial stress SIGRES is computed according to the radius from this integration point to the center of the cylinder.
In plane strain state (IANA=2) and generalised plane strain state (IANA=5), the stresses are the following ones:
- SIGMA(1,IPI) = $\sigma_x = \sigma_1 . cos² \alpha + \sigma_2 . sin² \alpha$
- SIGMA(2,IPI) = $\sigma_y = \sigma_1 . sin² \alpha + \sigma_2 . cos² \alpha$
- SIGMA(3,IPI) = $\tau = ½ (\sigma_2-\sigma_1) . sin 2\alpha$
- SIGMA(4,IPI) = $\sigma_L$ = SIGRES
where $\alpha$ is the angle between $\vec{r}$ and axis X and $\sigma_1$ & $\sigma_2$ the principal stresses in the plane (r,θ). In this case, $\sigma_1 = \sigma_{circ}$ = SIGRES and $\sigma_2 = \sigma_{rad}$ = ZERO.
In axisymmetric state (IANA=3):
- SIGMA(1,IPI) = $\sigma_r$ = ZERO
- SIGMA(2,IPI) = $\sigma_T$ = SIGRES
- SIGMA(3,IPI) = $\tau$ = ZERO
- SIGMA(4,IPI) = $\sigma_L$ = SIGRES
5 - Definition of the elements
| (3I5/8I5) | |
|---|---|
| NNODE | Number of nodes: 3, 4, 6, or 8 |
| NINTE | Number of integration points: 1, 3, 4, 7, or 9 |
| LMATE | Material |
| NODES(NNODE) | List of nodes |
Results
The mechanical Cauchy stresses are ordered as: $\sigma_x, \sigma_y, \tau_{xy}, \sigma_z$. These stresses are expressed in the global axis system.
