User Tools
Sidebar
This is an old revision of the document!
Table of Contents
Appendix 8: Water retention curves, water and air relative permeability curves and thermal conductivity function
Water Retention Curves
In this appendix, the different laws expressing the Water Retention Curves in FKRSAT.F are presented, along with their equations and parameters.
/!\ Not all laws are compatible with FKRSAT, only: /!\
155-119-120-126-127-128-171-172-173-174-175-180-197-95-198-196-176-177-199-194-182-629
| ISR = 0 - Saturated medium |
|---|
The saturation degree stays equal to one: \[S_w = 1\]
| ISR = 1 |
|---|
\[S_w = S_{r,field}-CSW1\left(\frac{s}{CSW3}\right)^{CSW2}\] The suction is defined as $s=p_a-p_w$ and $CSR3$ can be taken equal to $\rho_w.g.C^{ste}$.
| ISR = 2 |
|---|
\[ -\frac{s}{\rho_wg} = \begin{cases} -10.214\exp(-15.27S_w+6.062) & \quad \text{if } 0.1<S_w<1 \\ -10.214\exp(314.84S_w^2-78.24S_w+9.21) & \quad \text{if } 0<S_w<0.1 \end{cases}\]
| ISR = 3 |
|---|
\[ S_e(p_c)= \begin{cases} CSR3+\left(1+\left(\frac{p_c}{CSR1}\right)^{\frac{1}{1-CSR2}}\right)^{-CSR2} & \quad \text{if } p_c>0 \\ 1 & \quad \text{if } p_c \leq 0 \end{cases}\]
| ISR = 4 |
|---|
\[S_w = \begin{cases} CSR1 * ln\left(\frac{s}{10^6}\right) +CSR2 & \quad \text{if } 0.26 \text{ MPa}<s<222\text{ MPa} \\ S_{res} & \quad \text{if } s>222 \text{ MPa} \\ S_{r,field} & \quad \text{if } s<0.26 \text{ MPa}\end{cases}\]
| ISR = 5 - Van Genuchten formulation |
|---|
\[S_w = S_{res} + (S_{max}-S_{res})\left(1+\left(\frac{s}{CSR1}\right)^{CSR2}\right)^{-\left(1-\frac{1}{CSR2}\right)}\]
| ISR = 6 |
|---|
\[S_w = S_{res}+\frac{CSR3*(S_{r,field}-S_{res})}{CSR3+(CSR1*s)^{CSW2}}\]
| ISR = 7 |
|---|
\[S_w=\frac{CSR1 \log(s*10^{-6})+CSR2}{100} \\ \text{If } S_w<S_{res} \Rightarrow S_w = S_{res} \\ \text{If } S_w>S_{r,field} \Rightarrow S_w = S_{r,field}\]
| ISR = 8 |
|---|
\[S_w=\frac{CSR3}{\pi}\arctan\left(-\frac{s+CSR2}{CSR1}\right)+\frac{CSR3}{2}\] 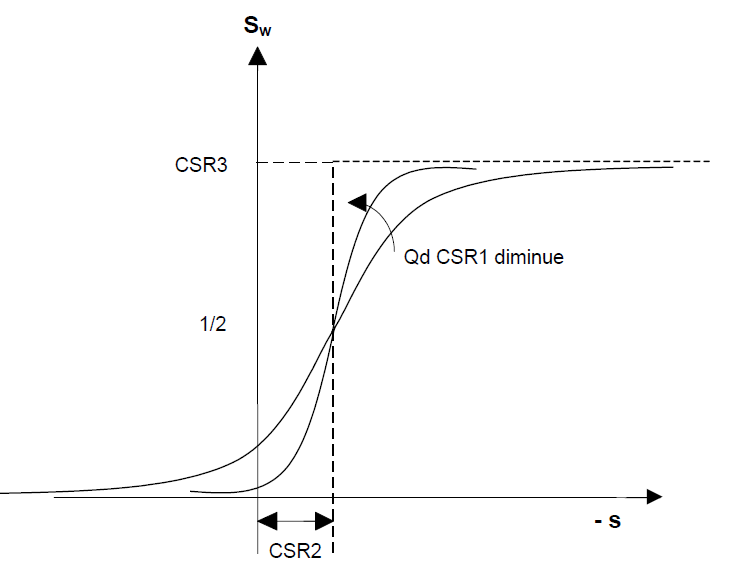
| ISR = 9 - Quasi-saturated soils (XL2) |
|---|
\[S_w= \left(1+ \frac{p_w}{p_a}\right)*S_{r,field}*\frac{1}{1+\frac{p_w}{p_a}*S_{r,field}*(1-HENRY)}\]
| ISR = 10 |
|---|
Comparaison eclipse
| ISR = 11 |
|---|
Comparaison eclipse
| ISR = 12 |
|---|
Comparaison eclipse
| ISR = 13 |
|---|
\[SATUR= CSW3*(DATAN(-(PC+CSW2)/CSW1)/PI+HALF)\]
| ISR = 14 |
|---|
Comparaison eclipse
| ISR = 15 |
|---|
Andra for swelling clay (MX80) \[SATUR = ((1D0+(PC/CSW3)**COEFM)**(-CSW1))*((1D0-PC/CSW4)**CSW2)\]
| ISR = 16 |
|---|
Andra for argilities - Van Genuchten \[COEFM = 1D0-1D0/CSW2\] \[SATUR = (1-CSW3-CSW4)*(1D0+(PC/CSW1)**CSW2)**(-COEFM)+CSW3\]
| ISR = 17 |
|---|
(EPFL-LMS, Lausanne)
Parameter correspondance:
CSW1=$\beta_h$
CSW2=$s_{hys}$
CSW3=$\theta_T$
CSW4=$\theta_e$
CSW5=RETINI
An elasto-plastic approach is used to describe the curve of retention of the soil. This implies two plastic mechanisms:
→ A mechanism activated during drying $f_{dry}=s-s_d=0$
→ A mechanism activated during the wetting $f_{wet}=s_d s_{hys} - s=0$
Where $s_d$ is the drying limit and $s_{hys}$ is a parameter defining the opening of the hydric hysteresis. When a mechanism is activated, $s_d$ evolves according to the following exponential law: $s_d=s_{d0}\exp(-\beta_h \Delta S_w)$ 
The effects of mechanical deformation and of temperature on the retention curve are considered through the evolution of the entering air suction: \[s_e=s_{e0}\exp(-\beta \Delta S_w)\left[1-\theta_T\log(T/T_0)-\theta_e \log(1-\varepsilon_v)\right]\] In order to characterize the initial degree of saturation inside the hydric hysteresis, the RETINI parameter is used. At the initial state, for a given suction, if RETINI = 0, the point is on the drying curve; if RETINI = 1, the point is on the wetting curve. RETINI can also take a value between 0 and 1. In that case, the saturation degree is determined using a linear interpolation between the drying curve and the wetting curve.
| ISR = 18 |
|---|
(EPFL-LMS, Lausanne)
Parameter correspondance:
CSW1=$s_{D0}$
CSW2=$\kappa_H$
CSW3=$\beta_H$
CSW4=$\pi_H$
CSW5=RETINI
The water retention curve is modeled using an elasto-plastic approach with kinematic hardening (ACMEG-s model, LMS, EPFL)  The yield surface delimiting the elastic domain takes the following form: \[f=\left\Vert ln\left(\frac{s}{s_D}\right)+\frac{1}{2}ln\left(\frac{s_{D0}}{s_{eH}}\right)\right\Vert - \frac{1}{2} ln \left(\frac{s_{D0}}{s_{eH}}\right)\] The saturation degree $S_w$ can be decomposed in an elastic part $S_w^e$ and a plastic part $S_w^p$: \[S_w = S_w^e+S_w^p\] The elastic part is defined by parameter $\kappa_H$ \[S_w^e=1- \frac{1}{\kappa_H}ln\frac{s}{s_{eH}}\] The plastic part is defined by: \[S_w^p=S_w^D-\frac{1}{\beta_H}\ln\frac{s}{s_D}\] The saturation degree cannot be higher than 1 or lower than $S_{res}$.
The yield surface delimiting the elastic domain takes the following form: \[f=\left\Vert ln\left(\frac{s}{s_D}\right)+\frac{1}{2}ln\left(\frac{s_{D0}}{s_{eH}}\right)\right\Vert - \frac{1}{2} ln \left(\frac{s_{D0}}{s_{eH}}\right)\] The saturation degree $S_w$ can be decomposed in an elastic part $S_w^e$ and a plastic part $S_w^p$: \[S_w = S_w^e+S_w^p\] The elastic part is defined by parameter $\kappa_H$ \[S_w^e=1- \frac{1}{\kappa_H}ln\frac{s}{s_{eH}}\] The plastic part is defined by: \[S_w^p=S_w^D-\frac{1}{\beta_H}\ln\frac{s}{s_D}\] The saturation degree cannot be higher than 1 or lower than $S_{res}$.
The entering air suction $s_{eH}$ evolves with the total volumic deformation: \[s_{eH}=s_e+\pi_H*\varepsilon_v\] In order to characterize the initial degree of saturation inside the hydric hysteresis, the RETINI parameter is used. At the initial state, for a given suction, if RETINI = 0, the point is on the drying curve; if RETINI = 1, the point is on the wetting curve. RETINI can also take a value between 0 and 1. In that case, the saturation degree is determined using a linear interpolation between the drying curve and the wetting curve.
| ISR = 19 |
|---|
- idem as ISR = 5 with the addition of AIREV in the van Genuchten formulation: \[S_w = \begin{cases} 1 & \quad \text{if } s < \text{AIREV} \\ S_{res}+(S_{max}-S_{res})\left(1+\left(\frac{s-AIREV}{CSR1}\right)^{CSR2}\right)^{-\left(1-\frac{1}{CSR2}\right)} & \quad \text{if } s > \text{AIREV} \end{cases}\]
| ISR = 20 |
|---|
\[SATUR = SRES+(SRFIELD-SRES)*(1D0+(PC/PR)**CSW2)**(-COEFM)\]
| ISR=21 |
|---|
Andra for Bentonite (UPC) \[COEFM = ONE-ONE/CSW2\] \[SATUR = (ONE+(PC/CSW1)**CSW2)**(-COEFM)*(ONE-PC/CSW3)**CSW4\]
| ISR = 22 |
|---|
Romera et al., 2011
| ISR = 23 |
|---|
Unconstant parameters, function of the porosity. For laws WADUA, CLEATF and WPROG. (François BERTRAND).
| ISR = 25 |
|---|
Van Genuchten with “true” air-entry pressure (aept). \[COEFM = ONE-ONE/CSW2\] \[SATUR = SRES+(SRFIELD-SRES)*(ONE+((PC-AEPT)/CSW1)**CSW2)**(-COEFM)\]
| ISR = 26 |
|---|
Double structure mechanism adsorption: \[e_w=e_{wM}+e_{wm}\] \[e_w=e_m \exp \left(-(C_{ads}s)^{n_{ads}}\right) + (e-e_m) \left[1+\left( (e-e_m)\frac{s}{A}\right)^n\right]^{-m} \] \[S_r=\frac{e_w}{n}\] $n$=porosity
CSR1 = $A$
CSR2 = $m$
CSR3 = $n$
CSR4 = $C_{ads}$
CSR5 = $n_{ads}$
| ISR = 27 |
|---|
\[SATUR = DEXP(-PC/CSW1)\]
| ISR = 50 - For Mothymar law |
|---|
\[S_w = 1 * \left(1+\left(\frac{s}{CSR1}\right)^{CSR2}\right)^{CSR3}\] \[S_{w,mic} = 1 * \left(1+\left(\frac{s}{CSR4}\right)^{CSR2}\right)^{CSR5}\]
| ISR = 52 |
|---|
Van Genuchten formulation (ISR.EQ.5) with independent CSW2 and COEFM \[S_w = S_{res} + (S_{max}-S_{res})\left(1+\left(\frac{s}{CSR1}\right)^{CSR2}\right)^{CSR3}\]
| ISR = 53 |
|---|
Van Genuchten model (ISR=5) with hysteresis implemented.
The main water retention curves (d=drying, w=wetting) are, according to the Van Genuchten model:
\[S_{ed} = S_{res} + (S_{max}-S_{res}) \left[1 + \left(\frac{s}{a_d}\right)^{n_d}\right]^{-m_d}\] \[S_{ew} = S_{res} + (S_{max}-S_{res}) \left[1 + \left(\frac{s}{a_w}\right)^{n_w}\right]^{-m_w}\]
The hysteresis is then defined by:
\[\frac{\partial S_{es}}{\partial s} (\text{wetting}) = \left(\frac{s_w}{s}\right)^b\left(\frac{\partial S_{ew}}{\partial s}\right) \text{ with } s_w = a_w \left(S_e^{-1/m_w}\right)^{1/n_w}\] \[\frac{\partial S_{es}}{\partial s} (\text{drying}) = \left(\frac{s_d}{s}\right)^{-b}\left(\frac{\partial S_{ed}}{\partial s}\right) \text{ with } s_d = a_d \left(S_e^{-1/m_d}\right)^{1/n_d}\]
And therefore:
\[S_e^{t+1} = S_e^t + \left(\frac{\partial S_{es}}{\partial s}\right)\times ds\]
The ISR=53 parameters are: CSRW1=$a_d$, CSRW2=$n_d$, CSRW3=$a_w$, CSRW4=$n_w$ and CSRW5=$b$
Water relative permeability
- IKW = 0 \[k_{rw} = 1\]
- IKW = 1 \[k_{rw} = CKW3 - CKW1 (1-S_{r,w})^{CKW2}\] Example: CKW1 = 2.207; CKW2 = 0.953; CKW3 = 1
- IKW = 2 \[k_e^{rel} (S_e) = \left(1+\left(S_{r,w}^{CKW1} - 1\right)^{CKW2}\right)^{-1}\] Example: Momas: CKW1 = -2.429; CKW2 = 1.176
- IKW = 3 \[k_{r,w} = \begin{cases} \exp(CKW1*S_w+CKW2*S_w^2) & \quad \text{if } S_w \geq S_{res} \\ k_{r,min} & \quad \text{if } S_w<S_{res} \end{cases} \]
- IKW = 4 \[k_{r,w} = \begin{cases} \frac{(S_w-S_{res})^{CKW1}}{(S_{r,field}-S_{res})^{CKW2}} & \quad \text{if } S_w \geq S_{res} \\ k_{r,min} & \quad \text{if } S_w<S_{res} \end{cases} \] Example: $CKW1 = 4$; $CKW2 = 4$; $S_{r,field} = 1$; $S_{res}=0.1$
- IKW = 7 \[k_{rw}=\sqrt{S_{rw}} \left(1-\left(1-S_{rw}^{\frac{1}{CKW1}}\right)^{CKW1}\right)^2\]
- IKW = 8 \[k_{rw} = S_{rw}^3\]
- IKW = 9 \[k_{rw}=\sqrt{S_{we}} \left(1-\left(1-S_{we}^{\frac{1}{CKW1}}\right)^{CKW1}\right)^2\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\] \[S_{rw,res}=CKW2\] \[S_{rg,res}=CKW3\]
Air relative permeability
- IKA = 0 \[k_{ra}=1\]
- IKA = 1 \[k_{ra} = (1-S_e)^{CKA1}(1-S_e^{CKA2})\] \[S_e=\frac{S_{rw}-S_{rw,u}}{1-S_{rw,u}}\] Example: CKA1 = 2; CKA2 = 5/3
- IKA = 2 \[k_{r,a}=CKA1\]
- IKA = 3 \[S_e = \frac{S_{r,w}-S_{r,u}}{1-S_{rw,u}} \\ \begin{cases} \text{If } S_e<0 \Rightarrow S_e = 0 \\ \text{If } 0<S_e<0.55 \Rightarrow k_{ra}=(0.55-S_e)^{CKA1}(1-S_e^{CKA2}) \\ \text{If } S_e>0.55 \Rightarrow k_{ra}=k_{rmin} \end{cases} \] Remark: \[k_{w,effectif}=k_{f,intrinsic}k_{rw} \\ k_{a,effectif}=k_{f,intrinsic}k_{aw}\]
- IKA = 6 \[k_{ra}=\sqrt{1-S_{r,w}}\left(1-S_{r,w}^{\frac{1}{CKA1}}\right)^{2CKA1}\]
- IKA = 7 \[k_{ra}=\sqrt{1-S_{we}}\left(1-S_{we}^{\frac{1}{CKA1}}\right)^{2CKA1}\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\] \[S_{rw,res}=CKA2\] \[S_{rg,res}=CKA3\]
- IKA = 8 \[k_{ra}=CKA2(1-S_{we})^{CKA1}\] \[S_e=\frac{S_{rw}-S_{rw,res}}{1-S_{rw,res}-S_{rg,res}}\]
Thermal conductivity
| ITHERM | $\Gamma_T$ |
|---|---|
| \[1\] | \[nS_w\Gamma_w+nS_a\Gamma_a+(1-n)\Gamma_s\] |
| \[2\] | \[CLT1*S_w +CLT2\] |
| \[3\] | \[CLT1 -\frac{CLT2}{1 + exp\left(\frac{S_w -CLT3}{CLT4}\right)}\] |
